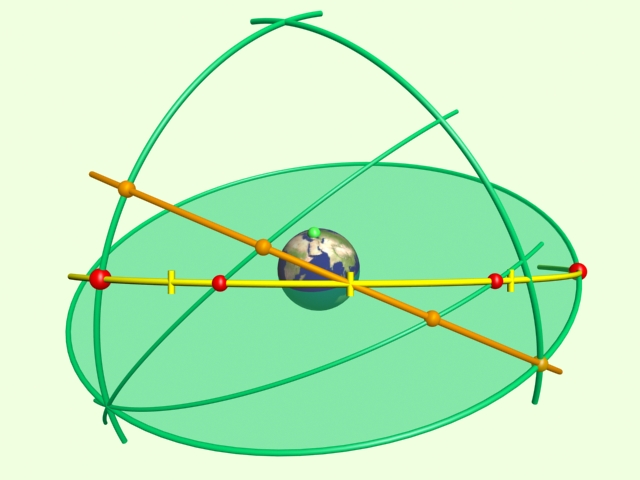
A regiomontanusi házrendszer sematikus ábrája
A Regiomontanus házsarkak kiszámítása
A Regiomontanus házsarkakat az Egyenlítőt egyenlő, 30°-os távolságokban metsző, az észak- és délpontokon áthaladó gömbi főkörök (pozíciókörök) ekliptikai metszéspontjai jelölik ki. Ezeknek a távolsága a Meridiántól, a Regiomontanus házrendszer definíciójából adottan ismert: 30° a 11. és a 9. ház illetve 60° a 12. és a 8. ház csúcsának kiszámítása esetén, az Egyenlítőn mérve. Mivel az Egyenlítőnek az A.O. és a Meridián közé eső szakasza mindig 90°-ot tesz ki, így pozícióköreink egyúttal az A.O.-tól való egyenlítői távolsága is ismert.

Először is vegyük észre, hogy maga a Horizont sem más, mint egy speciális pozíciókör; ebből következően, ha meg tudjuk állapítani, hogy egy adott pozíciókör hol metszi az Egyenlítőt, és ebben a pontban milyen szöget zár be a rá bocsájtott meridiánnal, akkor megállapítottuk, hogy mi lenne az A.O. és a F, ha az adott pozíciókör lenne az Ascendens; vagyis ekliptikai metszéspontját a már ismert Ascendens-számítási eljárással kaphatjuk meg.
Az adott pozíciókörre vonatkoztatott A.O.-t jelölje "a.o.", F-jét pedig "f".
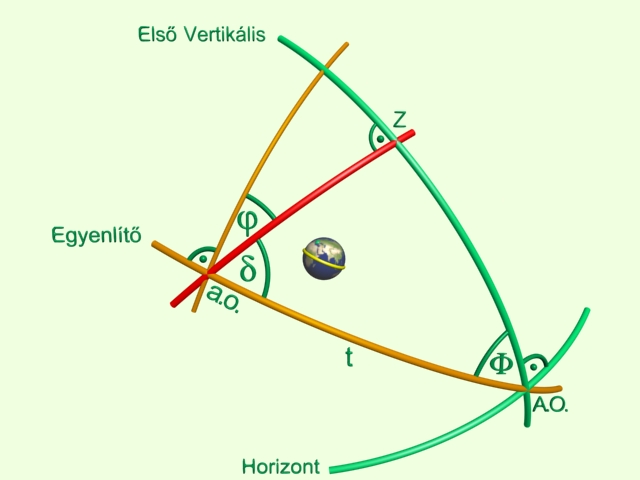
A Regiomontanus házrendszer definíciójából következik, hogy a "t" ívszakasz nagysága 30°vagy 60° lehet; ebből adódóan "a.o." pozíciója ismert: a.o. = A.O - t. Így az A.O. - Z - a.o. gömbháromszögből a f szöget az alábbiak szerint kaphatjuk meg.
$${ Cos( t ) = ctg( \delta ) * ctg( \Phi ) }$$ Mivel $${ \delta = 90°- \phi }$$ ezért: $${ \begin{align} Cos( t ) &= ctg( 90° - \phi ) * ctg( \Phi ) \\[0.25em] Cos( t ) &= \frac{tg( \phi ) * 1} {tg( \Phi )} \\[0.25em] Cos( t ) * tg( \Phi ) &= tg( \phi ) \\[0.25em] \end{align} }$$Az a.o. és a f ismeretében pedig, az előbbiekben már ismertetett Ascendens-számítási eljárással megkapjuk a 12. ház (t=30°) és a 11.ház (t=60°) csúcsait. Természetesen, ezek szemben lévő pontjai adják meg a 6. és 5. ház csúcsait.
A 8. és 9. házcsúcs kiszámolásához két dolgot kell figyelembe vennünk. Az egyik az, hogy ezeknél a "t" ívszakaszt a D.O.-tól kezdve kell mérnünk (a 8. házcsúcs esetén t=30° ill. a 9. házcsúcs esetén t=60°), mégpedig a D.O.-tól az ARMC felé, vagyis ebben az esetben: a.o. = D.O. + t. A másik, hogy míg az előző esetben f előjele F előjelével megegyező, ebben az esetben ellentétes vele. Ez egyszerűen belátható annak alpján, hogy az előző esetben a számításaink alapját képező pozíciókört úgy kapjuk meg, hogy a Meridiánt az Ascendens felé döntjük el, ebben az esetben viszont ellenkező irányban tesszük ezt meg.