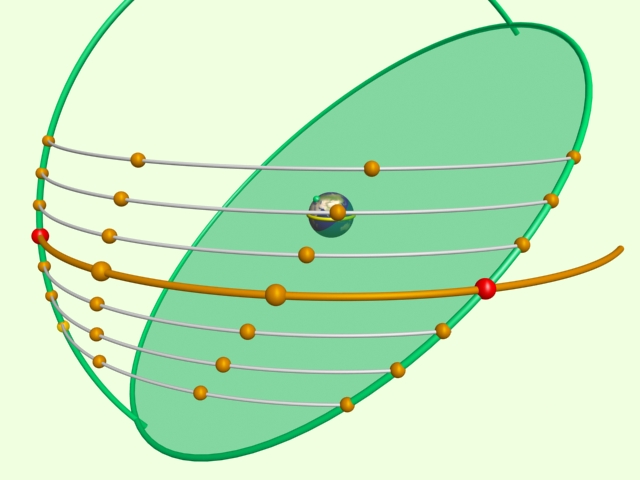
A placidusi házrendszer sematikus ábrája
A Placidus házsarkak kiszámítása
Placidus házszerkesztési elgondolása Ptolemaios egyik fejtegetésén alapul (a Tetrabiblos 3. könyvének "Az élet éveinek számáról" című fejezetéből). Ennek alapján Placidus úgy gondolta, hogy ha az egyes házcsúcsok az Egyenlítőt - mint Regiomontanus mondja - egyenlő arányban kell, hogy messék a Horizont és a Meridián egyes részei (pl. az AO és az ARMC) között, akkor ugyanilyen arányban kell metszeniük az Egyenlítővel párhuzamos valamennyi gömbi körnek a Meridián és a Horizont közé eső megfelelő részeit is.

Természetesen, az egyes házcsúcsok ott lesznek, ahol a fenti szerkesztési elv szerint megkapott gömbfelszíni görbék az Ekliptikát is metszik.
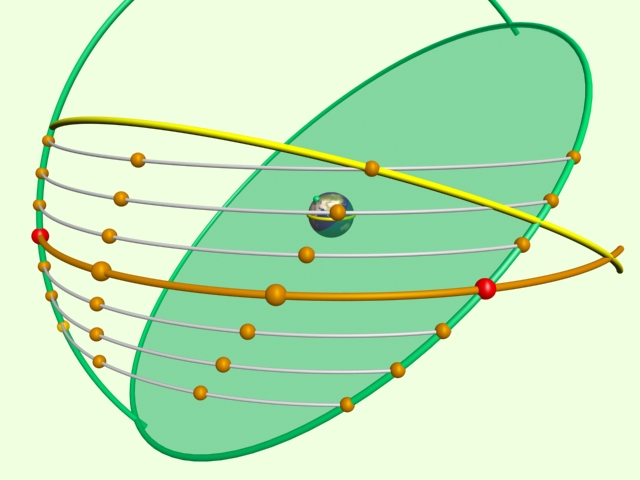
Egyszerűbben szólva, Placidus az összes Fél Nappali Ív és az összes Fél Éjjeli Ív megfelelő harmadoló pontjait összekötő vonalaknak az Ekliptikával való metszéspontjait keresi meg.
Ezzel kapcsolatban az első problémánk, hogy hogyan határozzuk meg az egyes S.D.A-k vagy S.N.A.-k nagyságát? Hiszen ezek nem gömbi főkörök mentén helyezkednek el, tehát szférikus trigonometriai ismereteink nem alkalmazhatóak a kiszámolásukra. Azonban a szélességi körök is, mint bármely más kör, 360°-ból állnak. Két meridián pedig ugyanakkora ívszakaszt fog közre az Egyenlítőn, mint az egyes szélességi körökön. Ennek alapján pedig már bármely félív nagysága kiszámolható.
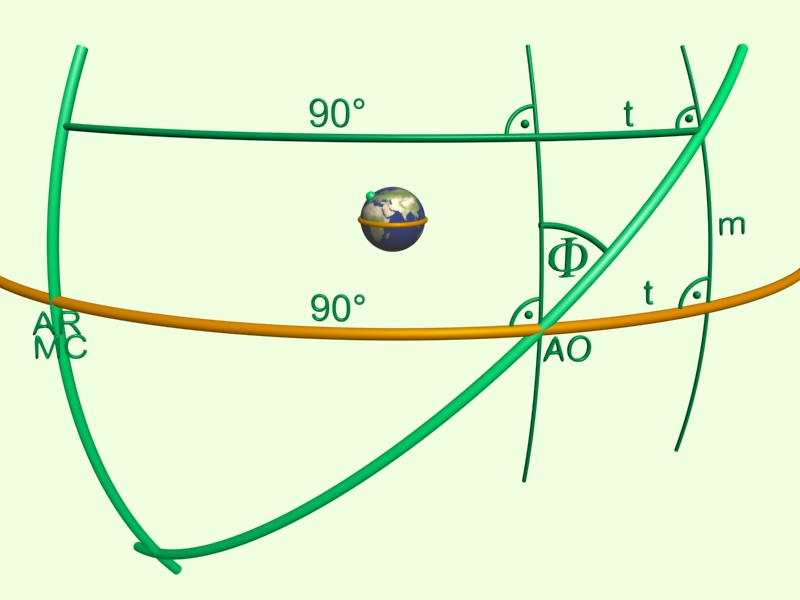
Látható, hogy északi F és északi m esetén az S.D.A. = 90°+t. (Északi F és déli m esetén S.D.A. = 90°-t lenne. Déli F esetében S.D.A = 90°+t, ha m déli, és 90°-t, ha m északi.) A t ívszakasz nagyságát a következőképpen kapjuk meg:
Az S.D.A. = 90°+t. Az S.D.A.-t már nem nehéz három egyenlő részre osztani, és az egyes házcsúcsok AR-ját kiszámolni. Így az egyes - egyenlőre még csak feltételezett! - házcsúcsok egyenlítői pozíciói a következők lesznek:
A kérdés már csak az, hogy az adott AR-val és m deklinációval rendelkező pont vajon rajta van-e az Ekliptikán?
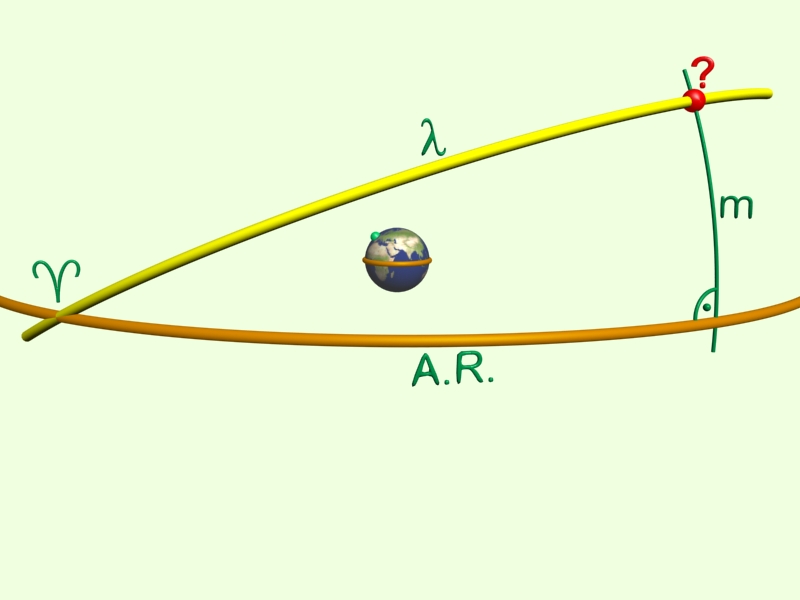
Ha igen, akkor az A.R. alapján a megfelelő ekliptikai pontot kiszámoló képletünkbe valamely feltételezett házsarok AR-jét helyettesítve, visszakapjuk m értékét:
Ha az így kapott n = m, akkor megtaláltuk a keresett házcsúcsot, és ekliptikai pozíciója (l) a szokott módon kiszámolható. Ha n nagyobb, mint m, akkor az Ekliptika, az adott AR értéknél, a harmodolópontunk felett helyezkedik el, ha kisebb, akkor pedig, természetesen, alatta.
Most már csak az a kérdés, hogyan határozzuk meg, hogy mekkora m helyes értéke? Sajnos, ezt nem tudjuk
egyetlen számolással kiszámolni. Legegyszerűbb, ha a következő eljárást alkalmazuk:
Ezt a számítási sorozatot addig végezzük, amíg n = m lesz. A ciklus igen gyorsan fogja közelíteni a helyes m értéket, kb. egy tucatnál többször aligha kell elvégeznünk, hogy fokperc pontosságú adatot kapjunk. (Két tucatszor elvégezve már fokmásodperc pontosságú adatot kaphatunk.) Azonban, sajnos az eljárást minden házcsúcsra (8., 9., 11., 12.) külön meg kell ismételnünk, mert az egyes házcsúcsok nem azonos szélességi körön helyezkednek el, hanem az Ekliptikán, így deklinációjuk, azaz a hozzájuk tartozó m értékek, különbözők.
Ez eddigiekből láthattuk, hogy a placidusi házsarkak deklinációja csak e és -e közötti értékű lehet - éppúgy, ahogy minden más módszer szerinti házsaroké is, hiszen rajta kell lenniük az Ekliptikán. Azonban, ha az e és -e deklinációjú S.D.A.-k megfelelő harmadolópontjain át felveszünk egy gömbi főkört, akkor az igen kis eltéréssel követni fogja a placidusi módszer szerint megszerkesztett gömbfelületi görbét. Minden lehetséges lehetőséget nem számoltám végig, de úgy tapasztaltam, hogy ez az eltérés még Hamburg földrajzi szélességén (55°30´) sem nagyobb 20´-nél, ezért nyugodt lélekkel mondhatjuk, hogy sehol sem nagyobb 1°-nál. (Hamburg szélességéig még fél foknál sem.) Bizonyos esetekben - például, ha olyan horoszkópról van szó, amelyet még nem pontosítottunk - ez a pontatlanság még megengedhető. Ugyanakkor a placidusi házcsúcsok pontos kiszámításában is használhatjuk ezt a módszert, mert a kapott adatothoz képest +/- 1°-os határon belül kell már csak tovább keresnünk.
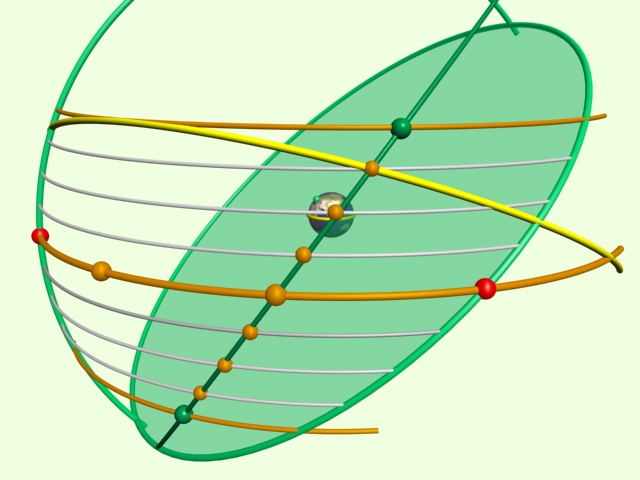
Az említett gömbi főkörről pár dolgot meg kell jegyeznünk:
Közelítő főkörünk felfogható egy olyan horizontnak, amelynek A.O.-ja ismert (az Egyenlítő megfelelő harmadolópontja), ennek megfelelően a hozzá tartozó ARMC is (A.O. -90°). Ha sikerül meghatároznunk a sarkmagasságát (f), akkor egy Ascendens-számítással megkapjuk az Ekliptikai metszéspontját is.
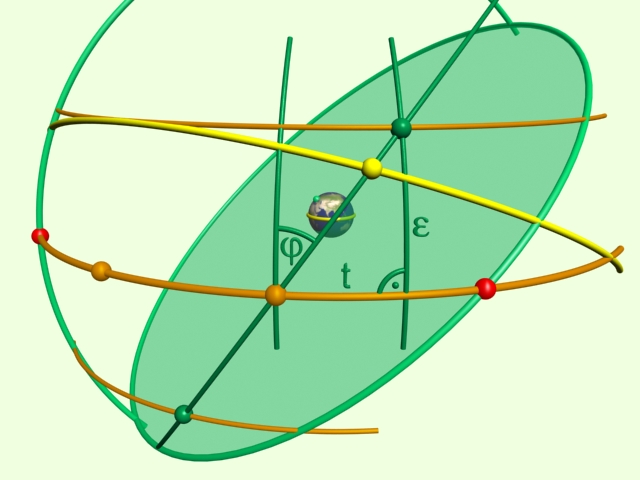
Az ábrán látható, hogy a t ívszakasz hossza egyenlő az egyenlítői harmadolópont Meridiántól mért távolsága és az S.D.A. harmadolópontjának Meridiántól való távolságának különbségével. Ez, a 9. és 11. ház esetében (S.D.A/3) -30°, a 8. és 12. ház esetében (S.D.A /3) *2 - 60°. (Ez utóbbi esetet ábrázolja a fenti kép is.) Ennek alapján már felírható:
Végezetül ne felejtsük el, hogy a 8. és 9. ház számításakor a f helyett itt is -f értéket kell vennünk.
A kapott ekliptikai pontból (l), a további pontosításhoz, vissza kell számolnunk a deklinációt (d). Ezt az alábbi - a Napier-szabályból egyszerűen levezethető - képlettel tehetjük meg:
Említettük, hogy a közelítő módszerrel kapott eredmény csak kiindulópontja lehet a pontos érték meghatározásának, illetve csak olyan esetben fogadható el, amikor a horoszkóp pontossága egyébként is kérdéses, vagy, még inkább, ha amúgy is bizonyosan pontatlan. Ezzel együtt nyomatékosan le kell szögeznünk azt is, hogy a nagy pontosságot igénylő számításoknál, mint például a direkciós számítások, a közelítő módszerrel kapott eredmény, lehetséges pontatlansága miatt, semmiképpen sem fogadható el. Fél fokos bizonytalanság eleve komolytalanná tenné mindenféle előrejelzési kísérletünkent, amint azt a megfelelő helyen látni is fogjuk.