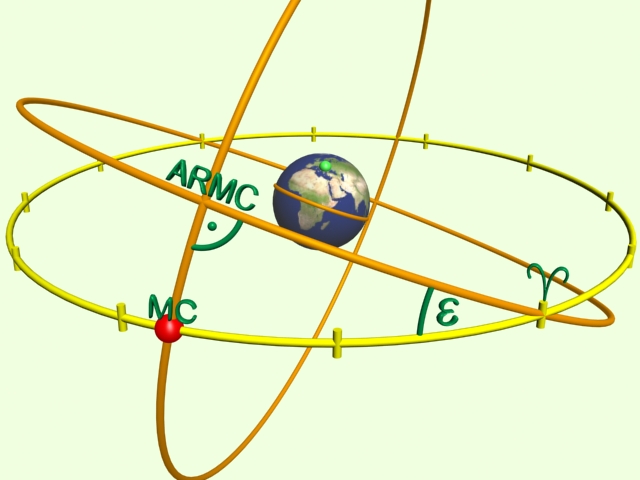
Az MC kiszámítása
Az MC kiszámításához ismernünk kell az ARMC fokokban kifejezett értékét, ennek meghatározását már a könyv elején elsajátítottuk. Az ARMC-t a meridián jelöli ki, azáltal, hogy metszi az Egyenlítőt; továbbhaladva pedig metszi az Ekliptikát is, ez utóbbi metszéspont az MC.

Attól függően, hogy az ARMC a Tavaszponthoz vagy az Őszponthoz van-e közelebb, a meridián ekliptikai és egyenlítői metszéspontjai és a megfelelő napéjegyenlőségi pont (a továbbiakban, röviden: N.P.) által alkotott gömbháromszöget vesszük számításaink alapjául. Ha az N.P.-től az ARMC-ig az óramutató járásával ellentétes irányban juthatunk el ebben a gömbháromszögben, akkor az N.P.-ARMC ívet pozitív szöggel fejezzük ki, ha az óramutató járásával megegyező irányban, akkor negatívval. (Erre azért van szükség, hogy a számítási műveletek közben az egymással kombinálódó szögfüggvények használata mellett is helyes eredményt kapjunk. A tangens függvény pl. 180 fokonként ismétlődő értékeket ad {tg(1°) = tg(181°)}. Ezzel a szemlélettel azonban kiküszöböljük az ebből adódó számítási kétértelműségeket.)
Így például, ha az ARMC értéke 181°, az N.P.-ARMC ív értékét 1°-nak vesszük, ha az ARMC 179° akkor -1°-nak; az N.P. az Őszpont. Ha az ARMC értéke 359° akkor az N.P.-ARMC ív -1°; az N.P. a Tavaszpont.
Az eddig elmondottakat az alábbi táblázattal foglalhatjuk össze:
| Az ARMC értéke | Az N.P. | Az N.P.-ARMC kiszámítása | Az N.P.-ARMC értéke |
| 0° - 90° | a 0° | ARMC | 0° - 90° |
| 90° - 180° | g 0° | ARMC - 180° | -90° - 0° |
| 180° - 270° | g 0° | ARMC - 180° | 0° - 90° |
| 270° - 360° | a 0° | ARMC° - 360° | -90° - 0° |
Adott tehát egy derékszögű gömháromszög, amelyben ismert egy oldal - az ARMC és az N.P. közti ív, ezt jelölje "A" -, egy szög - az Ekliptika hajlásszöge, amit e (epszilon) jelöl - és keresett az N.P. és az MC közötti ív, amit jelöljön "M".
A Napier-szabály szerint:
$$
cos( \varepsilon ) = ctg( 90 - A ) * ctg( M )
$$
Ennek átalakításai:
$$
\begin{aligned}
cos( \varepsilon ) &= tg( A ) * ctg( M ) \\[0.25em]
cos( \varepsilon ) / tg( A ) &= ctg( M ) \\[0.25em]
tg( A ) / cos( \varepsilon ) &= tg( M ) \\[0.25em]
\end{aligned}
$$
Az így kapott M értéket, hozzáaadjuk az N.P. megfelelő ekliptikai értékéhez ( 0° - vagy 360°, ha a kapott érték negatív -, illetve 180° ). Ezzel megkaptuk az MC-t.
Nézzük meg a számítás menetét az ábrán megjelenített példán.
Az ARMC = 305°, ennek megfelelően az N.P. a Tavaszpont, az N.P.-ARMC ívszakasz pedig -55°
$$
\begin{aligned}
\varepsilon &= 23°26´ \text{ (Efemeridából vett adat)} \\[0.25em]
cos( \varepsilon ) &= 0.9175234 \\[0.25em]
tg( -55° ) &= -1.428148 \\[0.25em]
tg( M ) &= -1.5565249 \\[0.25em]
M &= -57°17´ \\[0.25em]
MC &= 360°+ M = 302°43´ \\[0.25em]
\end{aligned}
$$
tehát az MC pozíciója: k 2°43´