A Napier-szabály és a Napier-analógiák
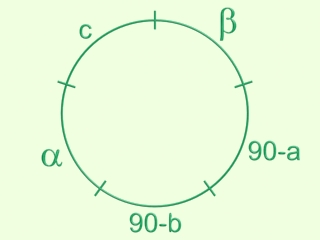
A Napier-szabály a derékszögű gömháromszögekre vonatkozó összefüggések megjegyzését könnyíti meg. Ezeket az összefüggéseket nem Napier fedezte fel, hiszen már jóval őelőtte is kiszámolták az asztrológusok a születési időből az MC-t és az Ascendenst, ehhez pedig mindenképpen szükségük volt ezekre, de Napier foglalta össze ezeket egyetlen szabályban.
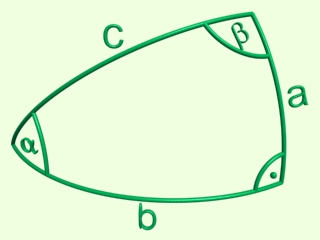
Vegyünk egy derékszögű gömbháromszöget.

Amennyiben olyan gömbháromszögtani számításokat kell elvégeznünk, amelyek nem vezethetők vissza derékszögű gömbháromszögekre, szükségünk lehet a Napier-analógiák ismeretére. (Ebben a könyvben ilyen számításokat nem fogunk használni, így a fejezetnek ez a része át is ugorható.)
A Napier-analógiák olyan egyenletek, amelyek a gömbháromszögek oldalai és szögei közötti összefüggéseket írják le. Ezek segítségével, ha a gömbháromszög három adata ismert, a többi is kiszámolható.
Legyen a gömbháromszög két oldala A és B, az általuk közbezárt szög pedig g, a és b a gömbháromszög másik két szöge. (Emlékeztetőül: a gömbháromszög oldala is kifejezhető a gömb közepétől mért szögben, sőt, a gömbháromszögtanban épp ez az általános.) Ekkor:
Hasonlóképpen járunk el akkor is, ha a gömbháromszög egyik oldala (c) és a rá illeszkedő két szög (a és b) ismertek:
$${
\begin{aligned}
\text{tg} \left( \frac{a+b}{2} \right) &= \frac{ \cos{ \left( \frac{\alpha-\beta}{2} \right) } }{ \cos{ \left( \frac{\alpha+\beta}{2} \right) } } * \text{ctg}\left( \frac{c}{2} \right) \\
\\
\text{tg} \left( \frac{a-b}{2} \right) &= \frac{ \sin{ \left( \frac{\alpha-\beta}{2} \right) } }{ \sin{ \left( \frac{\alpha+\beta}{2} \right) } } * \text{ctg}\left( \frac{c}{2} \right)
\end{aligned}
}$$
Ebből, az fentiekben már ismertetett módon:
$${
\left( a+b \right) /2 = X \text{ , } \left( a-b \right) /2 = Y \text{ : } \\
\begin{aligned}
a &= \left( X+Y \right) / 2 \\
b &= \left( X-Y \right) / 2
\end{aligned}
}$$
A Napier - analógiák levezetése megtalálható az interneten, ezen az oldalon.