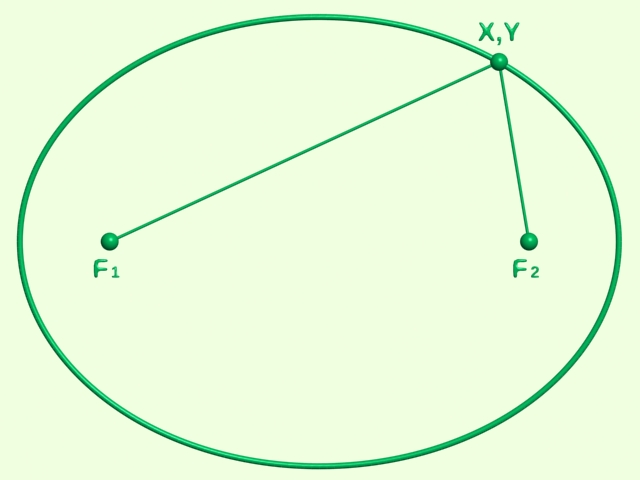
Az ellipszis az euklideszi sík azon pontjainak összessége, amelyek két meghatározott ponttól mért távolságának összege állandó. E két pontot az ellipszis fókuszpontjainak nevezzük.

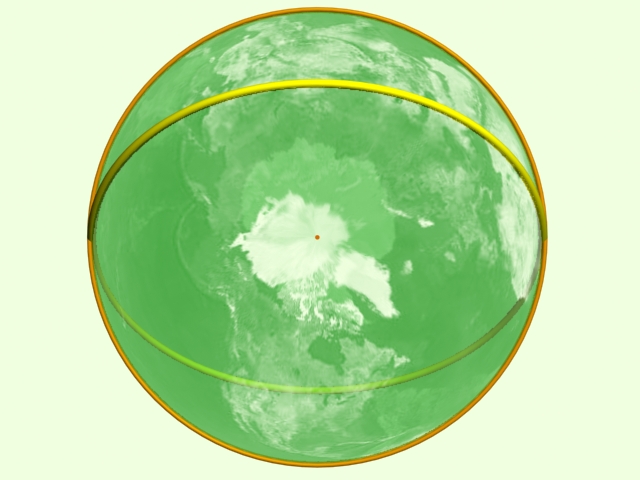
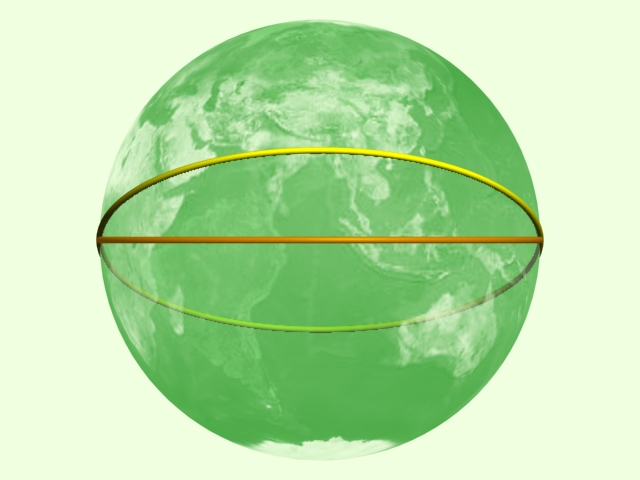
Számunkra az ellipszis ismerete azért szükséges, mert azon kör felülnézeti képe, amelyet egy a szöggel megdöntünk, ellipszist ad ki. Így például, az Ekliptika képe, ha az Egyenlítőre merőleges egyenes egy pontjából szemléljük, szintén ellipszis.