
A ponttól a síkszögekig
Az euklidészi sík:
Abszolút két dimenziósnak tekintett sík.
A pont:
Nulla dimenziósnak, minden kiterjedés nélkülinek tekintett absztrakt geometriai fogalom. Bármely geometriai idom, ideértve magát az euklidészi síkot is, végtelen számú pontból áll.
A szakasz:
Az euklidészi sík két pontját a legrövidebb úton összekötő pontok összessége.

Az egyenes:
A szakasz meghosszabbítása annak mindkét irányában, a végtelen felé.
A félegyenes:
A szakasz meghosszabbítása csak az egyik irányában, a végtelen felé.
Párhuzamos egyenesek:
Két olyan egyenes, amelynek nincs közös pontja.
Párhuzamos szakaszok:
Két olyan szakasz, amelyekre igaz, hogy a belőlük képzett egyenesek párhuzamosak.
Egymást metsző egyenesek:
Két olyan egyenes, amelyeknek van közös pontja. Két egyenesnek csak egy közös pontja lehet, ez a metszéspontjuk. A metszéspont a két egyenest két-két félegyenesre osztja fel.
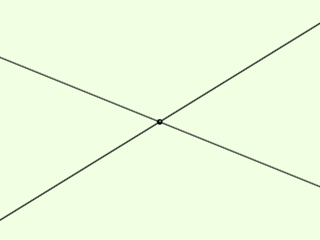
Egymást metsző szakaszok:
Két olyan szakasz, amelyeknek van közös pontja. Két szakasznak csak egy közös pontja lehet, ez a metszéspontjuk. A metszéspont a két szakaszt további két-két szakaszra osztja fel.
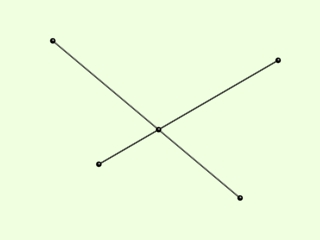
A kör:
A kör az euklidészi sík azon pontjainak összessége, amelyek egy meghatározott ponttól egyenlő távolságban vannak. Ez a pont a kör középpontja. A metszéspont és a kör bármely más pontja közé húzott szakaszt a kör sugarának nevezzük. (R vagy r)

A szög:
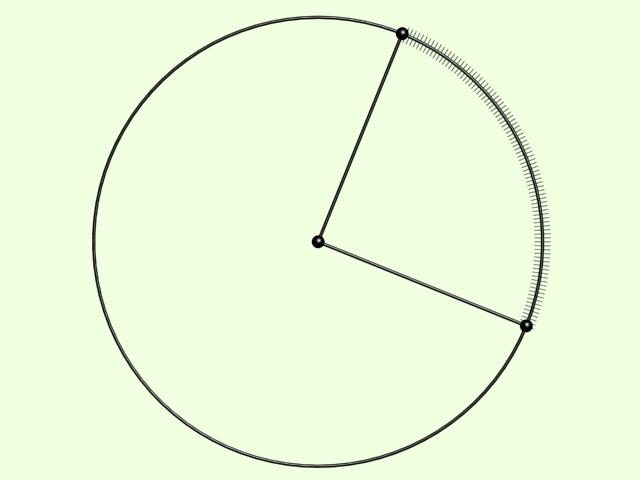
Két, egymást metsző egyenes metszéspontja köré tetszőleges sugarú kört rajzolhatunk. A metszéspont az egyeneseket négy félegyenesre osztja, melyek közül bármelyik kettő, a körrel alkotott metszéspontjai által, a körből egy-egy körívet jelöl ki. A teljes kör és ezen körív arányszámát nevezzük a körívet meghatározó félegyenesek - vagy, ha a félegyeneseket csak a körig tekintjük, akkor a körívet meghatározó szakaszok - által bezárt szögnek. A körívet meghatározó szakaszokat a szög szárainak nevezzük.
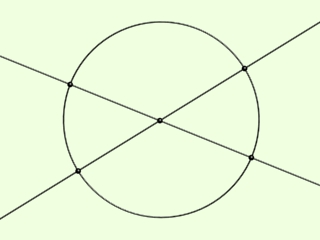
Az egyes szögeket a görög ABC betűivel jelüljük, amelyet a szög szárai közé írunk
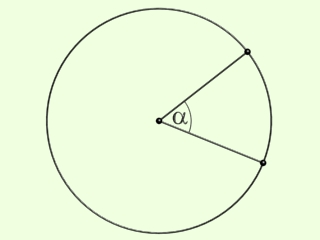
Két félegyenes a teljes kört két körívre osztja fel - ennek megfelelően két szöget határoz meg - amelyek együttesen a teljes kört adják ki.

Szögek egyenlőségei:
Két szög egyenlő, ha:
- Száraik egymással párhuzamosak

- Egyik száruk közös, vagy közös egyenesen fekszik, másik párhuzamos

Fokbeosztás:
A teljes kör felosztása 360 egyenlő részre.

Derékszög:
Két egyenest (vagy szakaszt) derékszögűnek mondunk, ha az általuk meghatározott kisebbik körív a teljes kör egynegyede, azaz 90 fok.
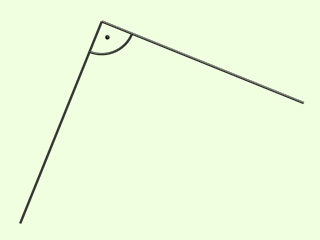
A derékszöget a két szára közé húzott kis körív és a szárak közé helyezett ponttal jelöljük.
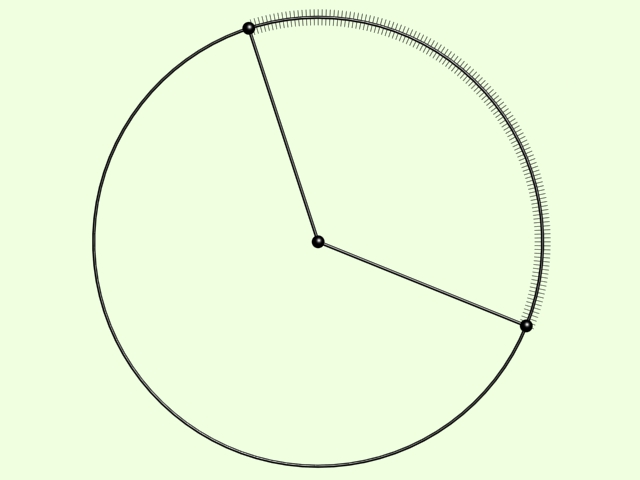
Hegyesszög:
Két egyenes vagy szakasz által meghatározott szögek közül az, amelyik 90 foknál kisebb.

Tompaszög:
Két egyenes vagy szakasz által meghatározott szögek közül az, amelyik 90 foknál nagyobb.
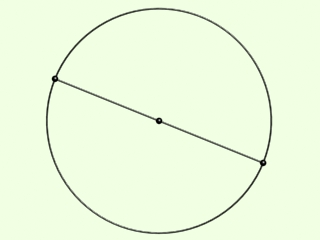
A kör átmérője:
Olyan szakasz, amely áthalad a kör középpontján, két végpontját pedig a kör jelöli ki. Ennek fele a kör sugara.
p (PI):
A kör átmérőjének és kerületének aránya, amely mindig azonos. Ennek megfelelően a kör kerülete: 2*R*p
Mivel a kör kerülete 2*R*p, és a körív a teljes kör egy bizonyos része, ezért az egyes köríveket - és, ebből eredően, a velük kifejezett szögeket is - meg lehet adni a 2*R*p valahanyad részeként. Mivel arányszámról van szó, amelyben az R mindig azonos, ezért el is hagyható. Így egy másik ívmértékhez jutottunk, a radiánhoz (Rad). A teljes, 360 fokos körív tehát 2p radián. Az egyes körívek ennek bizonyos részei, például a 90 fok 0.5p radián, a 45 fok 0.25p radián, és így tovább.
A teljes kör 2p radián, ennek fele p radián, ez egyenlő 180 fokkal, ezért 1 radián = 180/p fok.
A p értékének meghatározása
A p értékére Babiloniában 25/8 értéket vettek, ez akkoriban megfelelő pontosságnak számított. Archimedes a 22/7 és a 223/71 középértékét vette, ezzel 3 tizedesig pontos értéket kapott. Ő abból indult ki, hogy a kör kerülete a körbe írt és a kör köré írt szabályos sokszög kerülete közé kell, hogy essen, ennek alapján a PI értéke megközelíthető. (Ugyanakkor ehhez a számításhoz szükséges a sinus függvény értékeinek ismerete.) Később a PI értékére végtelen sorozatokat találtak, ezek közül nézzünk néhány egyszerűbbet:
Leibniz (német matematikus, 1646-1716) sorozata:
Wallis (skót matematikus, 1616-1703) sorozata:
Feltétlenül megemlítendők Euler-féle sorozatok:
Machin sorozata: